Figura 1. Dato un triangolo rettangolo, la tangente di un angolo è definita come il rapporto tra il seno e il coseno dello stesso angolo. In matematica, in particolare in trigonometria, la tangente è una funzione trigonometrica definita come la proiezione sull'asse del punto di incontro tra il prolungamento del secondo lato dell'angolo orientato e la retta che tange la circonferenza.. Nel terzo quadrante la tangente è positiva perché sia il seno che il coseno sono valori negativi. Quando l'angolo è pari a 270° la tangente non esiste perché il coseno è zero. Nel quarto quadrante la tangente è negativa perché il seno è negativo mentre il coseno è positivo. In π/2 (90°) e 3/2π (270°) la tangente non esiste.

Identidades trigonométricas con tangente, cotangente, secante y cosecantes La Prof Lina M3
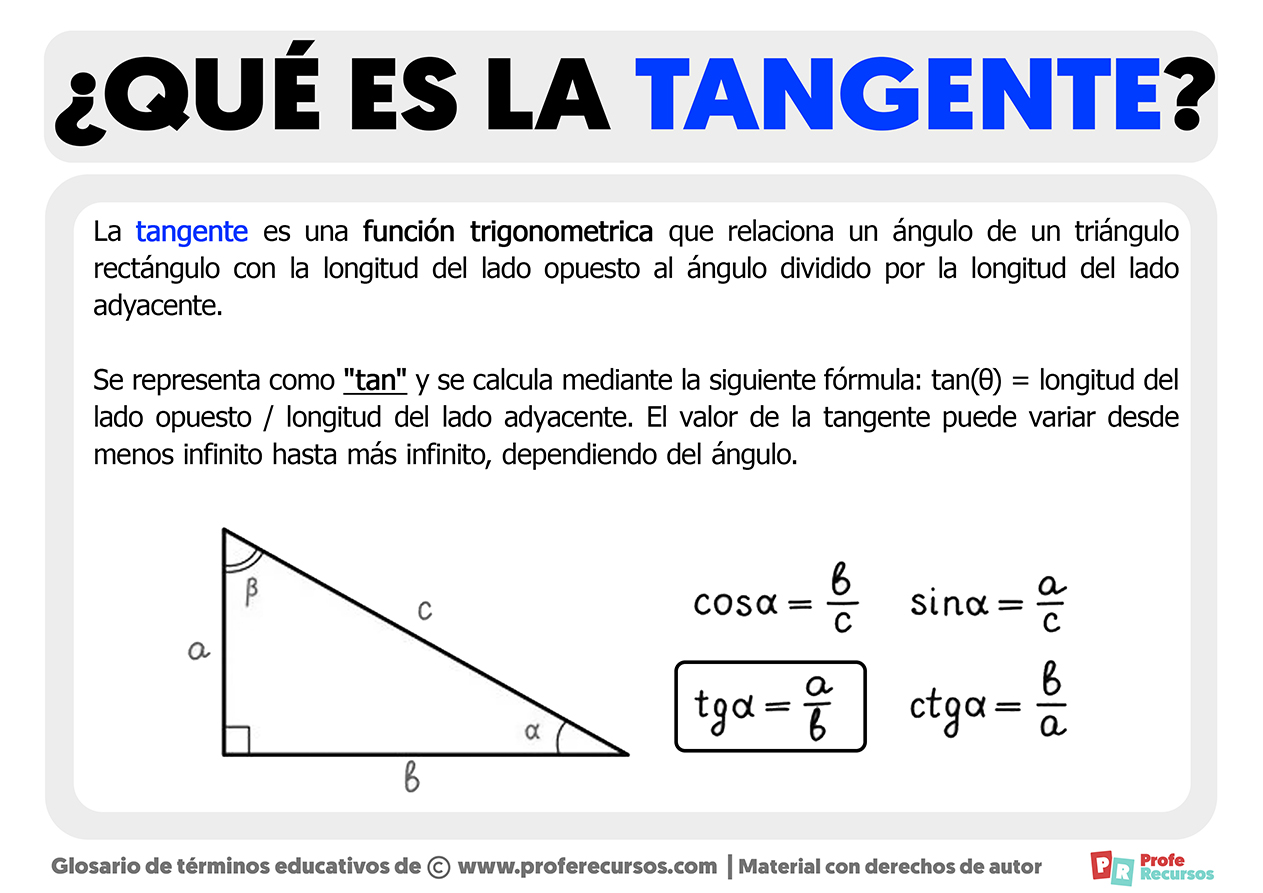
Qué es la Tangente Definición de Tangente

Retrouver graphiquement l'équation de la tangente 1S Exercice Mathématiques Kartable

Tangente no círculo trigonométrico A Raquel explicate A Raquel Explicate

Retta tangente ad una circonferenza YouTube
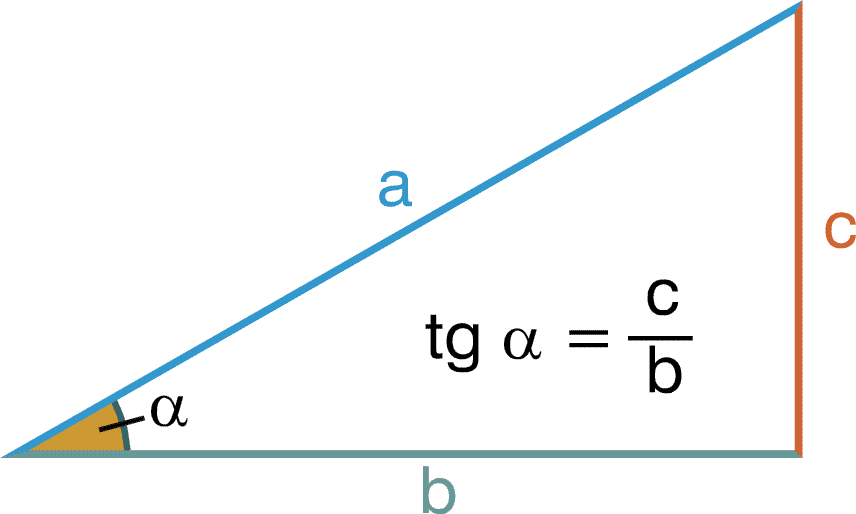
Tangente de un ángulo Enseñamos para que Aprendan Wiki Fandom

DERIVADA DE LA TANGENTE (Función Trigonométrica TANGENTE) YouTube

LA TANGENTE EN LA CIRCUNFERENCIA TRIGONOMÉTRICA YouTube
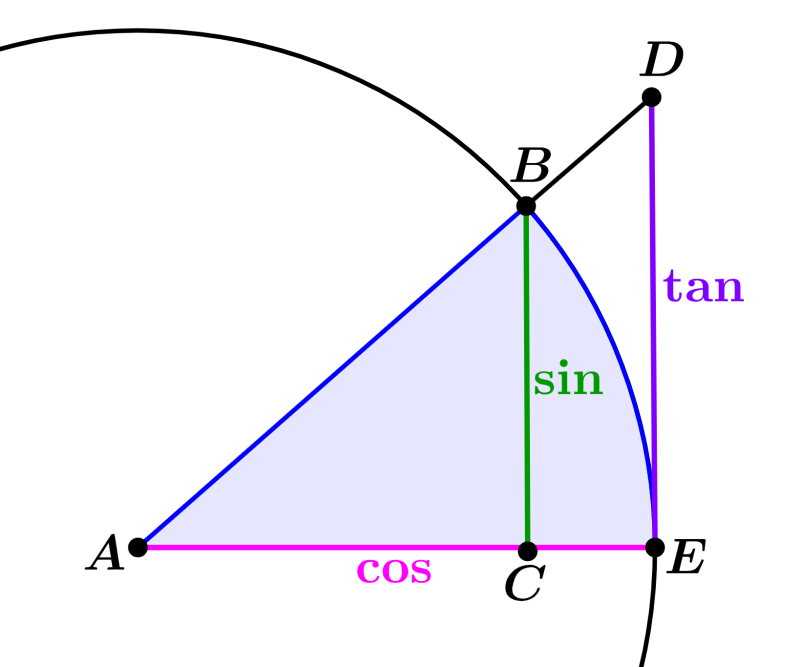
Tangente de un Ángulo Fórmulas y Ejercicios Neurochispas
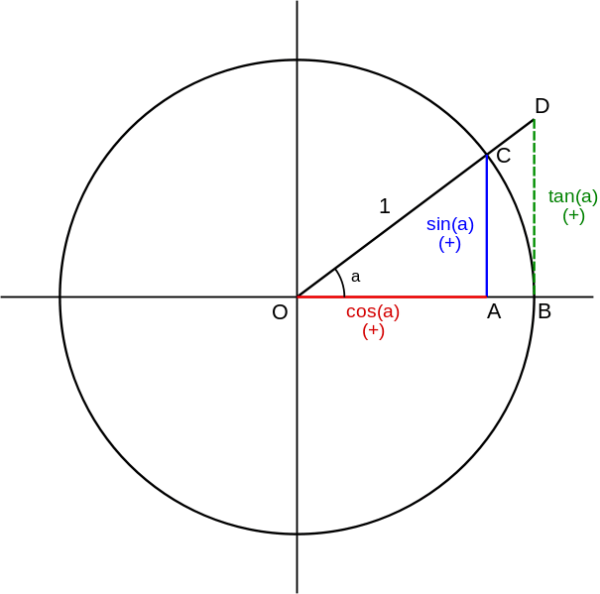
La funzione tangente SOS Matematica

LA TANGENTE DI UN ANGOLO significato geometrico. YouTube

Come Trovare l'Equazione della Tangente alla Curva
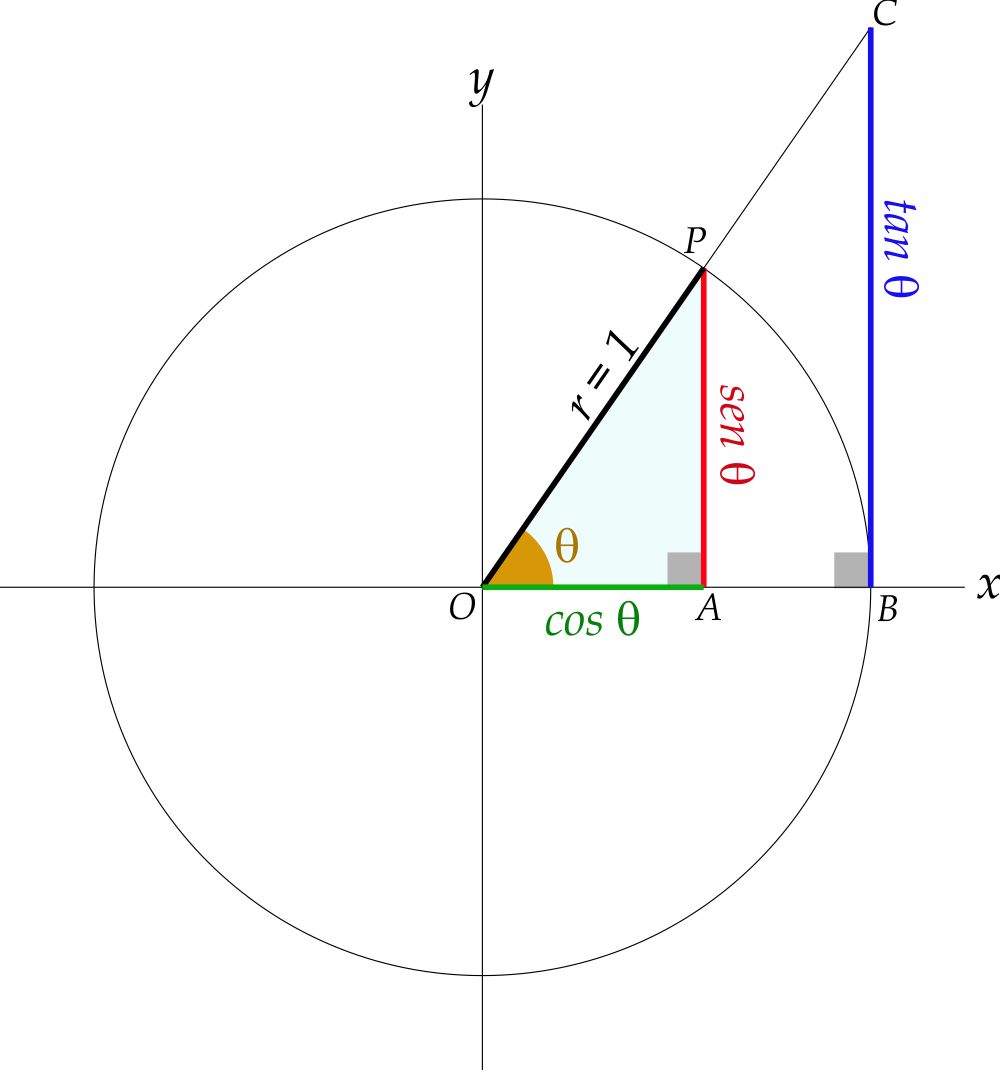
Le principali funzioni trigonometriche Rete di Eratostene

Tutorial tangente 1 YouTube

Arriba 104+ Foto Que Es La Tangente En Matematicas Alta Definición Completa, 2k, 4k 11/2023

Arquivos tangente do arco trigonométrico Casa da Matemática

équation de la tangente au cercle YouTube

Trigonometría, la tangente YouTube

Retrouver graphiquement l'équation de la tangente 1ère Exercice Mathématiques Kartable

RT00 1 Introducción a la RECTA TANGENTE a una FUNCION Bachillerato YouTube
A cosa serve la tangente nei vettori? La tangente nei vettori serve a determinare la pendenza di una linea retta o di una curva in un punto specifico. Ad esempio, se consideriamo una curva nel piano cartesiano, la tangente al punto di contatto con la curva ci fornisce la direzione in cui la curva si sta inclinando in quel punto.. L'arcotangente di x è definita come la funzione inversa tangente di x quando x è reale (x ∈ℝ). Quando la tangente di y è uguale a x: tan y = x. Allora l'arcotangente di x è uguale alla funzione inversa tangente di x, che è uguale a y: arctan x = tan -1 x = y. Esempio. arctan 1 = tan -1 1 = π / 4 rad = 45 ° Grafico di arctan. Arctan.